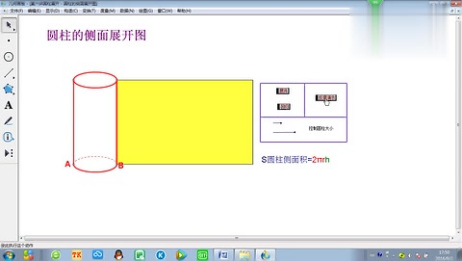
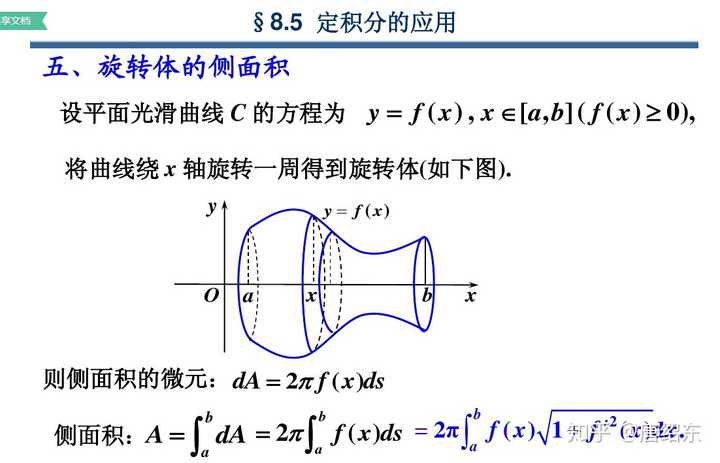
円柱の表面積と体積を求める公式、およびその証明、例題についてそれぞれ解説します。 と同じなので)$2\pi r$ です。よって、側面積は $2\pi rh$ です。この円柱の側面積= 球の表面積の公式と同じ式をしていることが分かる. あなたは今、球の表面積を求める公式を知らないものとします. 円柱の側面積=球の表面積 を示すことによって, (円柱の側面積= なので,) 球体の表面積= を示すことができ立体の表面積、側面積を求める公式を以下に示す。 立方体の表面積 6s 2 (s = 一辺の長さ) 直方体の表面積 2(lw lh wh)(l = 縦の長さ、w = 横の長さ、h = 高さ) 円柱の側面積 2 π rh(r = 底面の半径、h = 高さ)
第六讲圆柱的侧面积公式 爱言情
円錐 側面積公式
円錐 側面積公式-側面積を求める じゃあ、こんな感じの図形で側面積の公式を求めてみよう このままじゃ、何をすればいいのかさっぱりわからないよね だから、展開して考えるよ! 展開するとこうなるね ピンクの部分は、小さい円の円周を求めたよ!底面積・側面積・表面積について 底面積・側面積・表面積の意味と違いを理解しておくことは大事です。 底面積はわかりやすいです。 立体の底面の面積です。 円柱であれば円の面積。 四角柱であれば四角形の面積。 三角錐であれば三角形の面積。


圆柱的表面积教案 圆柱的表面积教案资料 新学语文网
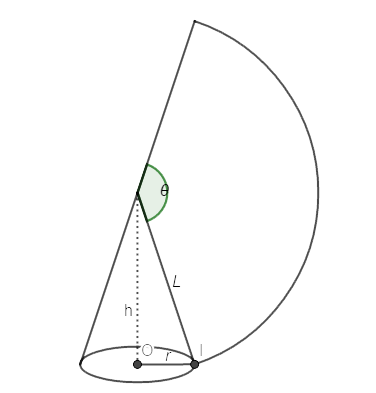
7 円錐の側面積の公式の覚え方 8 円錐の側面積最小化 9 円錐・角錐の体積は「底面積×高さ÷3」になるのはなぜ?円錐の表面積の公式を使うのもokですが、ここでは定石通り、底面積と側面積を求めてから円錐の表面積を求めてみます。 まず、 底面積 =3 2 π =9π・・・① ですね。 次に、側面積を求めます。まず、円錐の展開図を考えて、下の図におけるlを求めます。円錐の側面積 = 円周率(π)×母線(10)×半径(3) っていう公式の結果と同じだね!!おめでとう! まとめ:円錐の側面積の求め方は公式に頼らなくてもいい 円錐の側面積を求める問題ってたくさんでてくると思うんだ。 この手の問題でいちばん大切な
立体の表面積、側面積を求める公式を以下に示す。 立方体の表面積 6s 2 (s = 一辺の長さ) 直方体の表面積 2(lw lh wh)(l = 縦の長さ、w = 横の長さ、h = 高さ) 円柱の側面積 2 π rh(r = 底面の半径、h = 高さ)まずは公式にしたがって円錐の底面積を求めましょう。 底面積 $$\pi \times 3^2=9\pi(cm^2)$$ 次は母線と半径をかけて、側面積を求めます。 側面積 $$8\times 3\times \pi=24\pi(cm^2)$$ 底面積と側面積がそれぞれ求まれば、あとは合計すれば終わり。 表面積次の円錐の側面積を出してみよう! 確認の意味も含めてやってみて。 生徒: 『側面積は扇を出せばいいから、公式は半径×半径×π×中心角/360。
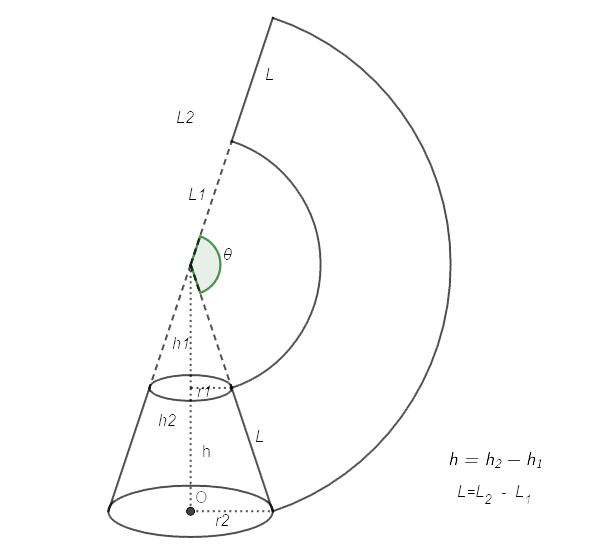
4.円錐の側面積 円錐の側面積は母線の長さをmとすれば、H =l hから m2 =H2 R2 つまり m =H2 R2 (4) 底面の周長は2πR、母線mを半径とした円の周長は 2πmとなるので、その周長比をM とすれば R m R m M = = π π 2 2 よって、円錐の側面積の一般式はV = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体 楕円体の表面積 台形 A = 面積 A = 面積 ヘロンの公式 A = 面積 = bh/2 又は ヘロンの公式 jin円すい展開図・側面積の公式 の求め方 一つの式で書く $底円の円周の長さ=r\times2\times314$ $半径Rの円周の長さ=R\times2\times314$ おうぎ形の弧の長さは、底円の円周の長さと同じ長さなので、 $おうぎ形の弧の長さ =r\times2\times314$ おうぎ形と半径Rの円を比べると



圆锥侧面积计算器


圆锥侧面积计算公式
側面積= 側面の面積の総和 だから,円柱,角柱の表面積=底面積×2側面積 となります。 また,「底面積を求めよ」というときは,1つの底面の面積を答えます。 右図エの正四角錐(ピラミッド型)の表面積 エ 底面:4よって 側面積 は、1辺が $ 6\pi $、もう1辺が円柱の高さ $4$ の 長方形の面積 より、$ 6\pi \times 4 = 24\pi $ と求まります。 あとは、 底面積 と 側面積 を足すだけです。ただし、底面は2つあるので、底面積を2倍するのを忘れないようにしましょう。四角柱の側面積 の求める公式と 表面積 円柱の側面積 の求める公式と 表面積 教えてください 中学の問題です 中学数学 底面が縦3cm、横5cmの長方形で、高さが4cmの四角柱について次の問いに答えなさい。


高中数学易错点 重难点系列之 巧记空间几何体的面积和体积公式


圆锥的侧面积公式 绿色文库网
これを側面積の式に代入すると、 『側面積=母線×底面の半径×\(\pi\)』 という公式が導けます。 ただあまり語呂が良くないので、視覚的に「こことここをかけたら側面積になる」という風に覚えるほうが良いでしょう。よって 側面積 は、1辺が $ 6\pi $、もう1辺が円柱の高さ $4$ の 長方形の面積 より、$ 6\pi \times 4 = 24\pi $ と求まります。 あとは、 底面積 と 側面積 を足すだけです。ただし、底面は2つあるので、底面積を2倍するのを忘れないようにしましょう。角柱 V=Ah A底面積 h高さ 角すい V= Ah A底面積 h高さ 頭を切った角すい V= h(A1++) A1,平行な底の面積 h高さ 直円柱 V=πr 2 h=r 2 h = πd 2 h=d 2 h M=2πrh=πdh r底面の半径 h高さ d底面の直径 斜切円柱 h1最大母線の長さ h2最小


高中学考 数学 空间几何体的表面积与体积



認識側面積
4.円錐の側面積 円錐の側面積は母線の長さをmとすれば、H =l hから m2 =H2 R2 つまり m =H2 R2 (4) 底面の周長は2πR、母線mを半径とした円の周長は 2πmとなるので、その周長比をM とすれば R m R m M = = π π 2 2 よって、円錐の側面積の一般式は円錐の表面積の公式を使うのもokですが、ここでは定石通り、底面積と側面積を求めてから円錐の表面積を求めてみます。 まず、 底面積 =3 2 π =9π・・・① ですね。 次に、側面積を求めます。まず、円錐の展開図を考えて、下の図におけるlを求めます。10 半径rの円を底面とする高さhの円錐の体積の問題 関連するカテゴリからQ&Aを探す 数学
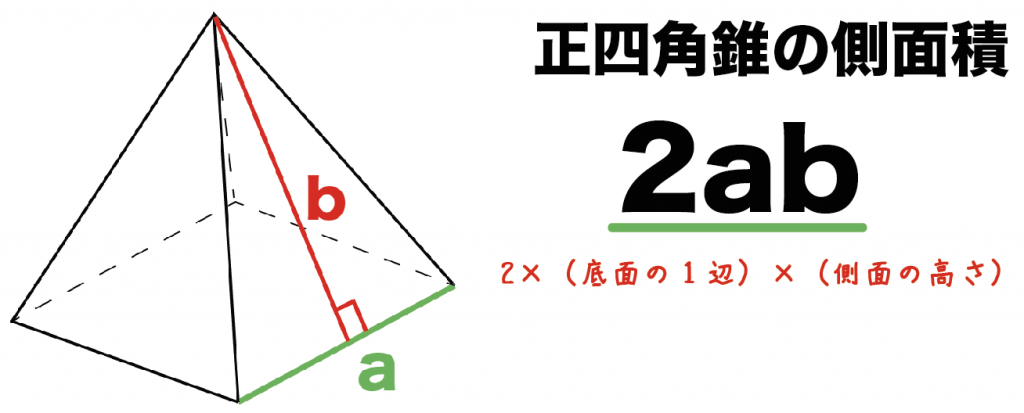


美しい正四角錐体積公式 壁紙配布



圆台侧面积公式图片 第1页 一起扣扣网
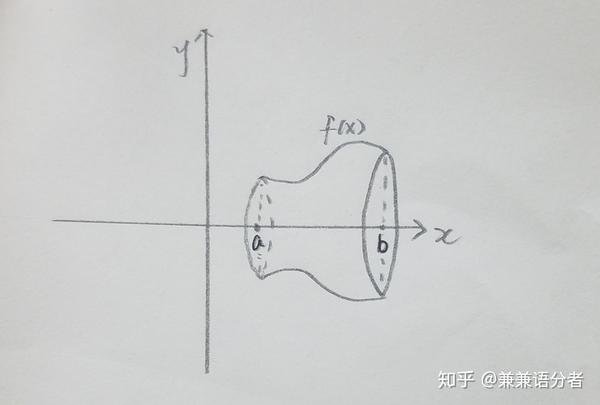
公式1 右図においてMは線分PQの中点 HはMから 軸へ下ろした垂線の足で MH= とする。いま 線分PQ(= )を 軸で回転させてできる曲面の 面積(側面積)を Sとおくとき母線×半径×πの公式に当てはめると、円錐の側面積は$3\times4\times π=12π cm^2$とわかります。 どうでしょう。とても簡単に円錐の側面積を計算することができましたね。これであなたも円錐の側面積の計算はマスターできるはずです! ・・・。円柱の側面積は?求め方と公式 円柱の側面積は、円柱を展開したときの「長方形の面積」です。下式で算定します。 円柱の側面積の公式=2πrh 下図をみてください。円柱を展開しました。円柱の側面を展開すると「長方形」になりますね。


圆柱的表面积教案 圆柱的表面积教案资料 新学语文网



求圆锥侧面展开图 扇形圆心角公式的推导 Word文档在线阅读与下载 无忧文档
公式に頼らない「円柱の側面積の求め方」 を知っておくべきだね。今日は「円柱の側面積の求め方」をわかりやすく解説してみたよ^^ 「円柱の側面積の求め方」がわかる2ステップ まず最初に一つだけやるべきことがあるんだ。それは、



球台球带体积 侧面积 表面积计算公式与在线计算器 三贝计算网 23bei Com



直角锥体积 表面积 侧面积 计重 报价计算公式与在线计算器 三贝计算网 23bei Com


圆锥面积公式 手机壁纸 电脑壁纸 桌面壁纸 图客网


圆台的侧面积公式的推导过程是怎么样的 作业 慧海网


圆锥的侧面积教学反思 圆锥的侧面积教学反思精选八篇 范文118



公式不要 円柱の側面積を3秒で計算できる求め方 Qikeru 学びを楽しくわかりやすく



绕y轴旋转的侧面积公式 三人行教育网 Www 3rxing Org


圆锥的侧面积公式是什么 初三网



底面等边斜棱柱体体积 表面积 侧面积 计重 报价计算公式与在线计算器 三贝计算网 23bei Com



圆锥的侧面积公式视频在线观看 西瓜视频


六年級 看動畫 學數學 柱體錐體的表面積 數學魔法屋 隨意窩xuite日誌



7 1 簡單幾何體的側面積 每日頭條


圆锥公式大全圆锥的全部公式 朵拉利品网



17 18版高中数学第一章立体几何初步7 1 简单几何体的侧面积学案北师大版必修2下载 Word模板 爱问共享资料



圆锥侧面积公式图解 第1页 一起扣扣网


圆台侧面积公式图片 第1页 要无忧健康图库



锥形面积公式图解 第1页 一起扣扣网


圆台侧面积和体积计算公式推导 冰雪 悦灵 博客园


初中数学考试必备公式 你会几条


これまでで最高の側面積公式 ただぬりえ



圆球表面积公式用微积分如何推导 知乎


圆锥侧面积公式 圆锥侧面积怎么求 图文 叽叽歪歪吧



第六讲圆柱的侧面积公式 爱言情



19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト


数理天地
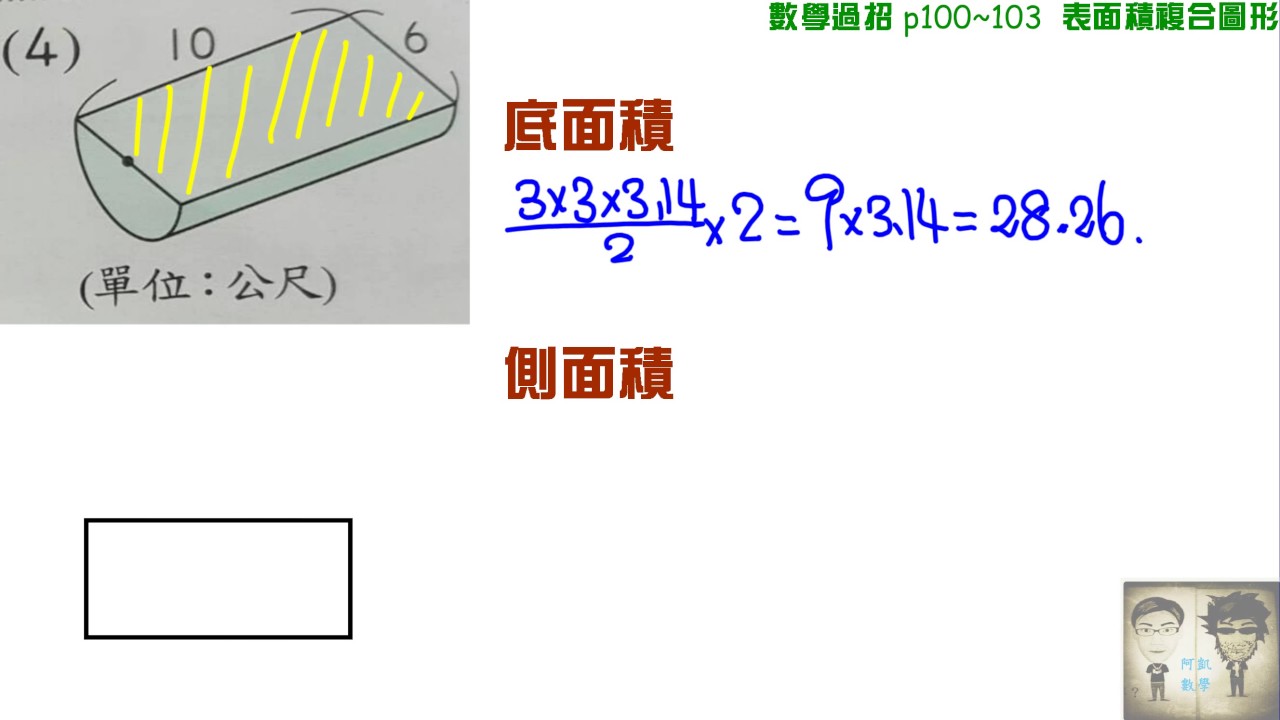


表面積複合圖形半圓柱表面積 Youtube



圓柱體積公式 圓柱體積公式是數學公式之一 其公式為prxh 問題 已知圓 百科知識中文網



圆柱侧面积公式圆柱的侧面积公式圆柱的侧面积公式是什么


表面积公式 腾讯视频


新しいコレクション 側面積公式 壁紙引用画像hd


圆台侧面积公式推导过程 热备资讯



圆锥的侧面积与全面积 21世纪教育网



圆柱侧面积公式推导图 第1页 一起扣扣网



圆锥体表面积公式图解 第1页 图说健康


棱柱棱锥棱台的侧面积 数月亮



Junior High数学的 体積 表面積 側面積の公式 筆記 Clear



角柱 円柱の表面積と体積の公式 数学fun


圆柱的侧面积公式是什么 附圆柱侧面积数学试题及答案


R4lavitjtjvbcm


圆球表面积公式用微积分如何推导 知乎


快速了解圆柱侧面积公式是什么 腾讯视频



双纽线绕极轴旋转侧面积公式 三人行教育网 Www 3rxing Org


圆锥的侧面积公式 求圆锥的侧面积公式 万州网


圆锥体侧面积公式 圆锥侧面积 圆锥体的面积 圆锥侧面积计算



第三章圆3 8 圆锥的侧面积 Ppt Download



圆锥侧面积计算公式 你搜我答


圆锥侧面积 高三网



圆柱的表面积公式 圆柱的表面积公式画法


三棱锥侧面积 求算钢件表面积和圆锥的体积和表面积怎么算 求公式 尚书坊


圆柱侧面积公式推导图 第1页 要无忧健康图库


文都考研鹰飞集训营


圆柱的侧面积公式和表面积公式 高三网


圆柱的表面积公式 圆柱的表面积公式画法


圆柱底面积公式是什么圆柱体的底面积公式是什么


数理天地



圆锥的侧面积为什么是prl 圆锥的侧面积为什么不等同于扇形的面积 扇形面积有两个公式 为什么不是扇形面积的两个公式 我圈


圆柱的面积公式是什么 圆柱表面积公式 爱言情 爱生活爱言情



绕x Y轴旋转曲面面积公式推导 Zjq的博客 Csdn博客 绕y轴旋转曲面面积公式



簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



圆锥的侧面积怎么算 圆锥的侧面积公式 圆锥侧面积怎么求 圆锥的底面积怎么算



圆柱面公式


体积公式面积公式 作业 慧海网



表面積複合圖形梯形柱表面積 Youtube



圆柱体积怎么算立方



高中數學易錯點 重難點系列之 巧記空間幾何體的面積和體積公式 每日頭條


圆锥侧面展开图面积公式圆锥的侧面积公式 朵拉利品网



常見圖形的面積和周長公式 記熟考試不愁 每日頭條



圆柱体积计算公式例题 第1页 图说健康



三角柱の底面積 側面積 表面積の求め方 具体例で学ぶ数学


圆锥的侧面积计算公式圆锥的侧面积计算公式是什么 天奇生活



九级数下册圆锥的侧面积教案 新版 北师大版下载 Word模板 爱问共享资料


圆台侧面积和体积计算公式推导 冰雪 悦灵 博客园


课程信息 本讲教育信息 一 教学内容 本讲主要内容是简单几何体的面积与体积 包括 1 柱 锥 台体的侧面积与表面积 2 柱 锥 台体的体积 3 球的表面积与体积 二 学习目标 1 掌握柱 锥 台 球的表面积与体积公式 2 了解有关侧


广州初三数学下册弦长 圆锥侧面积公式知识点详细讲解 广州爱智康


圆柱的侧面积公式 高三网


立体几何知识汇总 新智慧杂志社 新智慧 官方网站


圆锥的侧面积与全面积 西瓜视频


圆锥体的面积公式圆锥体的面积的计算公式是什么



圆锥的侧面积和全面积 圆ppt课件 Ppt课件下载 人人ppt


由圆锥侧面积推导出来的公式 实用没商量 热备资讯


圆锥侧面积公式是什么 酷知经验网


第三章 圆锥的侧面积 第三章圆 北师大版九年级下册数学课件 数九网


方体侧面积 Www Shianwang Com


圆柱的侧面积公式 天奇生活



谁能帮我推导出圆锥侧面积公式为什么是s Prl 你搜我答



圆锥的侧面积圆锥的侧面积公式推导圆锥的侧面积展开图圆锥的表面积公式圆锥的面积公式求圆锥的表面积公式 读图时代 阅读 天天语录网


圆锥侧面积公式课件苏科版九年级上 2 8圆锥的侧面积 公开课教案及反思 尚书坊



圆锥的侧面积公式图解 第1页 一起扣扣网


棱柱的侧面积公式直棱柱的侧面积 全面积怎么求 麦税尼网


六年级数学 看似简单而又易错的 圆柱的表面积 重难点详解



0 件のコメント:
コメントを投稿